[AI] Convex Optimization (볼록 최적화) / Convex, Non-Convex

Convex란?

• Convex란 '볼록한'이라는 뜻으로 수학에서 Convex를 대상이 집합(set)인지, 함수(function)인지에 따라 개념이 다르다.
• Convex Optimization은 목적함수 및 제약 조건 함수가 Convex Function 에 속하며, 동시에 문제의 범위에 해당하는 Domain이 Convex Set으로 정의된 경우에 해당한다.

Convex Function

• 흔히 우리가 볼록 함수라고 말하는 함수이다.

  • 아래로 볼록한 함수만 Convex function 이라고 한다.

  • 위로 볼록한 함수는 아래로는 '오목'한 함수이므로 Concave function이라고 한다.

    

• 함수 위의 임의의 두 점을 연결하는 선을 그래프에 그었을 때, 그 선이 아래 그림과 같이 함수 그래프의 위쪽만을 지나가면 이 함수는 Convex한 함수라고 할 수 있다.

  

• 수식으로 표현하면 다음과 같다.

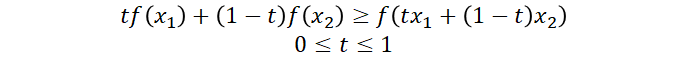
• 반면, 함수 위의 임의의 두 점을 연결하는 선이 함수의 아래를 지난다면 이는 Non-Convex 함수이다.
  

  

Convex Set

• Convex 한 집합을Convex Set이라고 부른다.
• Convex 집합은 집합이 이루는 공간 내의 두 점을 연결한 선분이 그 집합 안에 포함되는지, 포함되지 않는지에 따라 Convexity가 갈린다.
  

  

• 오른쪽의 경우 임의의 두 점 x와 y를 잇는 선분이 set의 바깥에 나와있어 Convex 하지 않다고 할 수 있다.

Convexity와 딥러닝

• 딥러닝은 매우 복잡한 다변수 함수의 최적해를 경사 하강법을 통해 찾는 것이다.

• 경사 하강법을 사용할 때, convex 함수와 non-convex 함수에서 탐색한 해는 큰 차이를 갖는다.

  

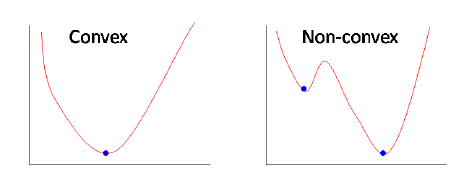
• convex 함수의 경우, 우리가 딥러닝에서 경사 하강법을 통해 찾는 최저점이 단 하나 존재한다. 이 점을 전역 최적해Global Minimum이라고 한다.

• non-convex 함수는 무한히 넓은 함수 공간에서 여러 곳의 지역 최저점 Local minima을 갖는다. 위 함수에서 이로 인하여, 경사 하강법을 시작하는 위치에 따라 서로 다른 최저점을 향해 결과가 수렴하게 된다. non-convex 함수의 문제는 우리가 어디가 전역 최적해인지를 알 수가 없다는 것이다. 이로 인해 non-convex 한 문제를 딥러닝으로 해결하려고 하면 학습이 잘 되지 않고 좋지 않은 지역 최저점에 갇히는 등의 문제가 발생한다.

→ 더 나은 지역 최저점을 찾기 위해 경사 하강법을 보완해 AdaGrad, RMSprop 등 다양한 Optimizer들이 연구되었다.

참고

• https://skyil.tistory.com/33
• https://kim-hjun.medium.com/convex-optimization-1-convex-function-set-eee8e65252b6
• https://www.researchgate.net/figure/Convex-and-nonconvex-functions-A-function-g-is-a-convex-function-if-domain-of-g-is-a_fig4_226717592