반응형
단층 퍼셉트론의 한계
선형 분류기linear classifier의 한계
- 퍼셉트론은 선형 분리 불가능한 상황에서 일정한 양의 오류가 발생한다.
- 예) XOR 문제에서 75% 정확도 한계
다층 퍼셉트론의 특징 공간 변환
퍼셉트론 2개를 사용한 XOR 문제 해결
- 퍼셉트론①과 퍼셉트론②가 모두 +1 → ㅇ부류
- 퍼셉트론①과 퍼셉트론②가 모두 +1 이 아님 → ㅁ 부류

1. 퍼셉트론 2개 병렬 결합
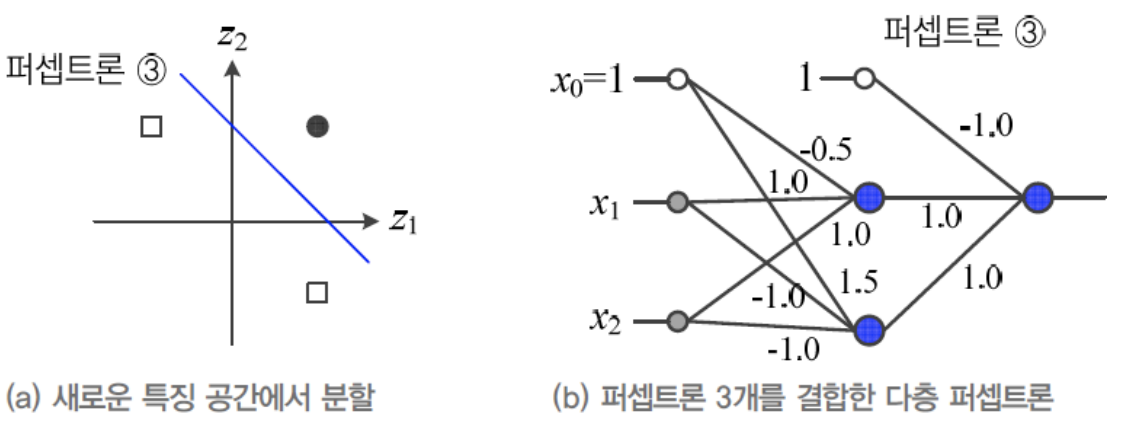
- 원래 공간 𝐱 = (𝑥1, 𝑥2)^T를 새로운 특징 공간 𝐳 = (𝑧1, 𝑧2)^T로 변환
→ 새로운 특징 공간 𝐳에서 선형 분리 가능

- 사람이 수작업 특징 학습을 수행한 것과 유사함 ← 표현학습
2. 추가 퍼셉트론 1개 순차 결합
- 새로운 특징공간 𝐳을 선형분리를 수행하는 퍼셉트론③을 순차 결합하면, 오른쪽의 다층 퍼셉트론이 됨
XOR 훈련집합 분류 테스트
- 위의 다층 퍼셉트론으로 XOR 훈련집합 분류해보기
- (𝑥1, 𝑥2)^T
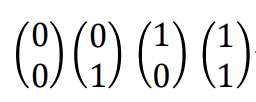
- 퍼셉트론①
- (0,0) : -0.5 x 1 + 1 x 0 + 1 x 0 = -0.5
- τ(-0.5) = -1
- (0,1) : -0.5 x 1 + 1 x 0 + 1 x 1 = 0.5
- τ(0.5) = 1
- (1,0) : -0.5 x 1 + 1 x 1 + 1 x 0 = 0.5
- τ(0.5) = 1
- (1,1) : -0.5 x 1 + 1 x 1 + 1 x 1 = 1.5
- τ(1.5) = 1
- (0,0) : -0.5 x 1 + 1 x 0 + 1 x 0 = -0.5
- 퍼셉트론②
- (0,0) : 1.5 x 1 + (-1) x 0 + (-1) x 0 = 1.5
- τ(1.5) = 1
- (0,1) : 1.5 x 1 + (-1) x 0 + (-1) x 1 = 0.5
- τ(0.5) = 1
- (1,0) : 1.5 x 1 + (-1) x 1 + (-1) x 0 = 0.5
- τ(0.5) = 1
- (1,1) : 1.5 x 1 + (-1) x 1 + (-1) x 1 = -0.5
- τ(-0.5) = -1
- (0,0) : 1.5 x 1 + (-1) x 0 + (-1) x 0 = 1.5
→ 퍼셉트론①과 퍼셉트론②에 의해
- 원래 공간 𝐱 = (𝑥1, 𝑥2)^T → 새로운 특징 공간 𝐳 = (𝑧1, 𝑧2)^T로 변환
- (𝑧1, 𝑧2)^T

- 퍼셉트론③
- (-1,1) : 1 x (-1) + 1 x (-1) + 1 x 1 = -1
- τ(-1) = -1
- (1,1) : 1 x (-1) + 1 x 1 + 1 x 1 = 1
- τ(1) = 1
- (1,-1) : 1 x (-1) + 1 x 1 + 1 x (-1) = -1
- τ(-1) = -1
- (-1,1) : 1 x (-1) + 1 x (-1) + 1 x 1 = -1
→ 해당 다층 퍼셉트론은 XOR 훈련집합에 있는 4개 샘플을 제대로 분류한다!
참고
반응형
'Artificial intelligence' 카테고리의 다른 글
| [AI] 평균 제곱 오차(MSE), 교차 엔트로피 오차(CEO), 로그우도(NLL) 계산 방법 (0) | 2021.12.03 |
|---|---|
| [AI] K - 최근접 이웃 (KNN)을 이용한 Iris 데이터셋 다중 클래스 분류 (0) | 2021.10.29 |
| [AI] 단층 퍼셉트론 (Single-layer Perceptron) (0) | 2021.09.23 |
| [AI] 검증집합과 교차검증을 이용한 모델 선택 알고리즘 / 데이터 확대와 가중치 감쇠 (2) | 2021.09.11 |
| [AI] 과소적합(underfitting)과 과잉적합(overfitting) / 바이어스(bias)와 분산(variance) (0) | 2021.09.10 |



